Differential Phase Contrast
Visualization and measurement of electric and magnetic fields at the atomic scale are vital in materials science development, as they directly impact electronic properties and materials applications (e.g., in memory technology or optoelectronics). Differential phase contrast (DPC) imaging in scanning transmission electron microscopy (STEM) allows for the examination of fields present inside and outside a specimen with resolutions only limited by the instrument's capabilities.
Introduced by Dekkers and de Lang [N. H. Dekkers and H. de Lang, Optik 41, 452 (1974)], DPC relies on the displacement of the center-of-mass (COM) of the illumination intensity at the detector plane (also known as a convergent beam electron diffraction (CBED) pattern or a Ronchigram). This lateral shift is due to the electron probe momentum change induced by and negatively proportional to the local electric field.
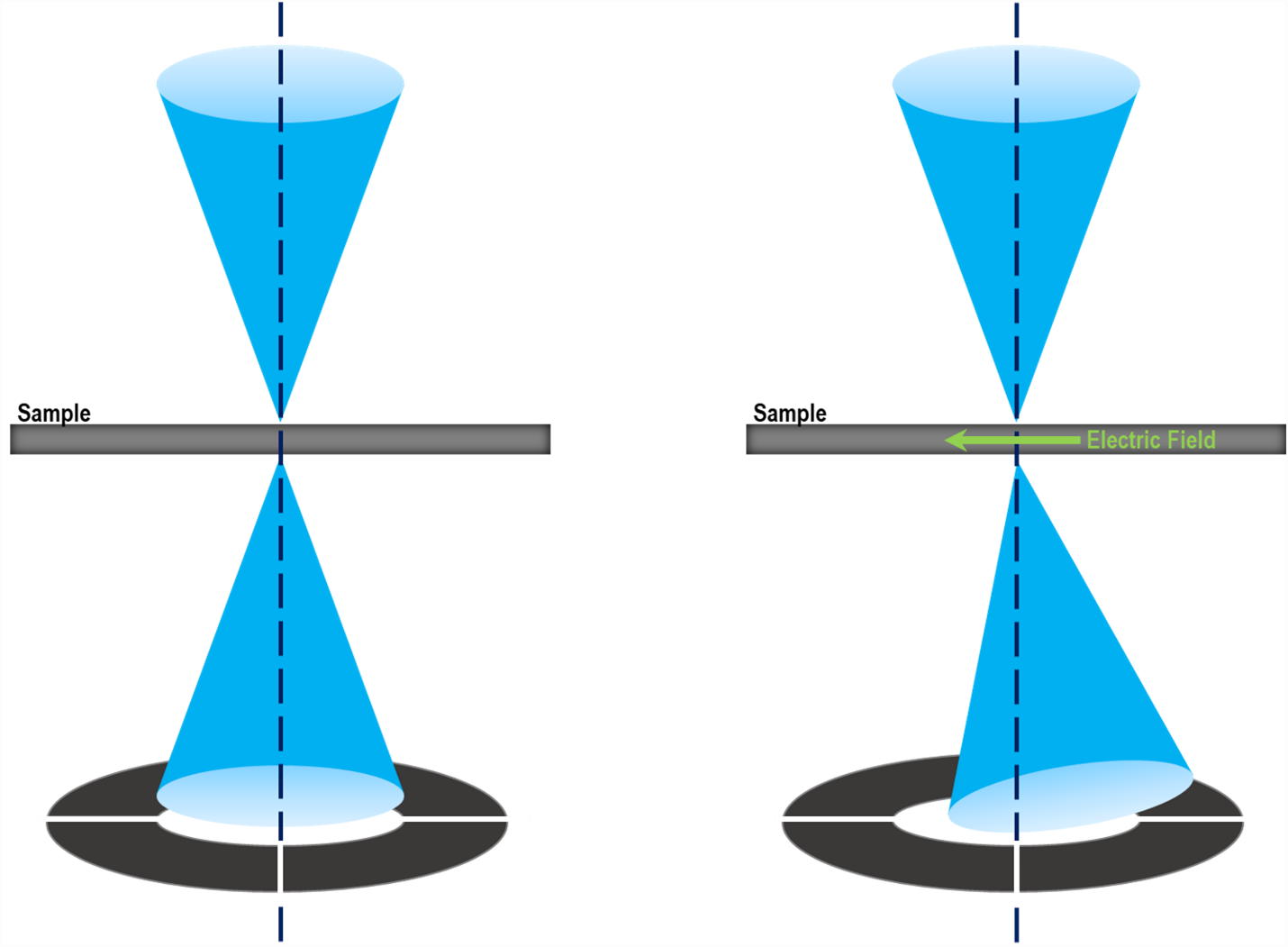
For non-magnetic samples, assuming small electric field variation through the beam path and minimal electron beam broadening as it passes through the specimen thickness, one can apply this linear relationship and use the measured beam shift to calculate the local electric field:
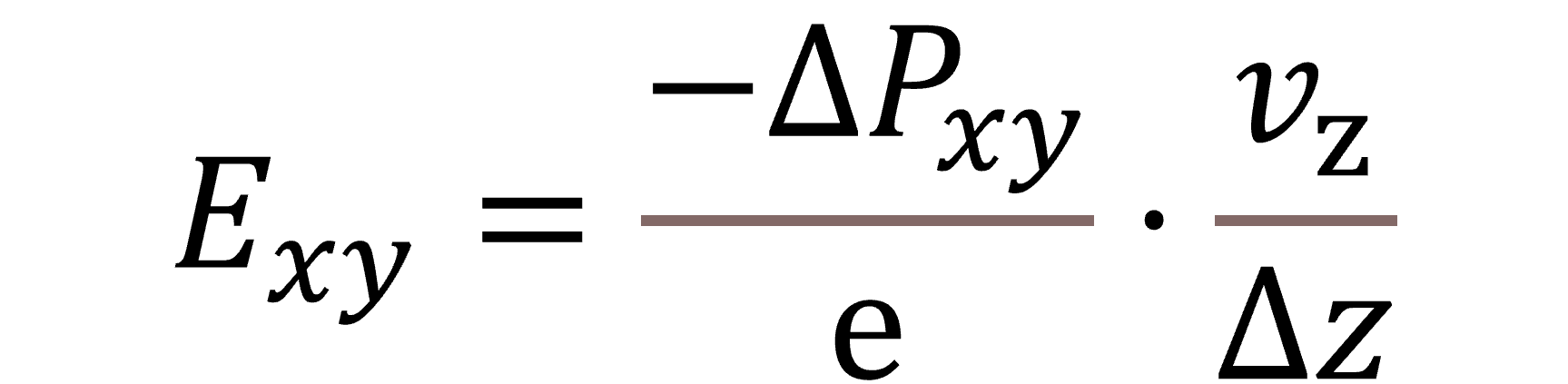
ΔPxy: change in the momentum of the electron beam, Exy: electric field, Δz: sample thickness, vz speed of electrons along the beam direction.
Once the electric field is calculated, one can also determine the charge density by calculating its divergence (according to Gauss's law, the divergence of the electric field is proportional to the charge density).
Conventional DPC imaging consisted of installing physical segmented STEM detectors in an electron microscope and measuring the difference of intensity falling on the opposing segments to measure the beam shift (1977). In such a configuration, selecting the proper camera length to ensure enough signal falls onto each segment at each probe position is vital, and the changes in intensities within each segment are not captured, as each segment integrates the signal over its entire region. Another drawback is the limitation of information transfer efficiency over several spatial frequencies (Optik, 54, 83-96, 1979). 4D STEM DPC overcomes these limitations by recording the entire diffraction pattern at each probe position. With the commercialization of aberration-corrected STEM and high-speed direct detection pixelated cameras, 4D STEM DPC imaging is a popular method for atomic resolution electric field measurements in thin specimens. It can be done in DigitalMicrograph®, as shown in the flowchart below:

4D STEM Data Collection Considerations for DPC
As with any electron microscopy technique, the microscope setup and the specimen are critical for DPC electric field measurements. In this case, convergent beam electron diffraction (CBED) patterns are recorded at each STEM probe position. Then, image processing is applied to measure the central beam shift in each 4D STEM data cube pattern to calculate the electric field.
Convergence angle: In an ideal case, the STEM probe should be significantly smaller than the scale of the electric field variation. Probe size (the spatial resolution) is determined by the convergence angle (condenser aperture and lens configurations). A larger convergence angle gives a smaller STEM probe (better spatial resolution) and vice versa. For atomic resolution DPC, the sample potential can be treated as linear when the probe size is smaller than the feature size. In this approximation, a phase proportional to the strength of the sample potential is measured, and the resulting diffraction is the original illumination disc uniformly shifted. If the probe size is larger than the feature to be measured, the DPC signal is caused by a shift and intensity redistribution in the original illumination. This signal includes information about short and long-range potentials and can be deconvoluted by applying frequency filtering.
Camera length: Select a camera length that allows you to record the full central beam in the CBED. A larger camera length spreads the disk over a larger number of pixels, resulting in less signal per camera pixel. Camera length should also be considered when selecting the convergence angle.
Specimen thickness: The measured electric field can be affected by samples with thicknesses larger than a few nanometers, as the assumption of a slight variation of the electric field through the beam path and minimal electron beam broadening as it passes through the specimen thickness is no longer valid in such cases.
DPC calculations in DigitalMicrograph
The sample data we use was provided by the researchers at the Molecular Foundry (Berkeley, CA, United States) and can be downloaded here. Energy-filtered 4D STEM diffraction data was collected at 300 kV, with a GIF Continuum® K3® IS system in electron counting mode, pixel size of 0.2 Å, and pixel dwell time of 0.00169 s.
DPC calculations in DigitalMicrograph are done on a 4D STEM diffraction data (CBED) using the Differential Phase Contrast technique and palette (screenshot below):

- Determine the beam displacement vector components (two orthogonal directions on the sample plane, x and y). There are two options available here:
- Center of mass (CoM) calculations or cross-correlation:
- CoM: DigitalMicrograph calculates the CoM for each diffraction pattern (each probe position), compares it to a reference CoM position (calculated from the entire dataset), and outputs the x and y shifts.
- Cross-correlation: DigitalMicrograph cross-correlates (with an optional user-defined numerical filter) each diffraction pattern (each probe position) to the central pattern in the 4D STEM data and outputs the x and y shifts.
- Virtual segmented detectors: This is similar to the conventional DPC using physical segmented STEM detectors. Instead of installing the detector on the microscope, the user designs a virtual detector (containing multiple annuli and segments) in DigitalMicrograph. The software then calculates the sum of the pixel intensities in each diffraction pattern for each segment. Then, it outputs the user-defined signals (any math applied to signals from the individual segments).
- Center of mass (CoM) calculations or cross-correlation:
- Calculate the beam displacement vector map and divergence
Select the two orthogonal components and click on Calculate vector displacement. DigitalMicrograph outputs a vector map, with intensity and color at each pixel corresponding to the magnitude and direction of the beam displacement vector, respectively. Lastly, select this vector map and click on Calculate divergence map. Based on the above equation, these outputs can be used to calculate the electric field and charge density.
Acknowledgments
Christopher Addiego, Wenpei Gao, and Xiaoqing Pan (University of California Irvine, USA) provided consultation for developing and implementing the DPC technique in DigitalMicrograph. We would also like to thank Jim Ciston (Molecular Foundry, Berkeley, CA, USA) for providing the example dataset and Roberto dos Reis (Northwestern University) for constructive feedback.